Wichtige Gesetzmäßigkeiten bei Graphen & ihre Eigenschaften im Überblick 

Arithmetische Eigenschaften von Eckengraden - Handshake Lemma Warum man beim Haus vom Nikolaus unten links oder rechts jeweils mit dem Zeichnen beginnen oder enden muss ? Arithmetische Eigenschaften von Eckengraden _ Handshake Lemma.pdf (1.95MB)

Arithmetische Eigenschaften von Eckengraden - Handshake Lemma
Warum man beim Haus vom Nikolaus unten links oder rechts jeweils mit dem Zeichnen beginnen oder enden muss ?

Arithmetische Eigenschaften von Eckengraden _ Handshake Lemma.pdf (1.95MB)

Inhalt im Überblick

Zusammenhang bei Graphen

Arithmetische Eigenschaften von Eckengraden - Handshake Lemmma

Zusammenhang bei Graphen

Zusammenhang meint im Kontext der Graphentheorie jene Struktur des Graphens, bei welcher alle Knoten direkt über indirekt über mehrere Kanten miteinander verbunden sind. Daraus resultiert, dass jeder Knoten sowohl bei ungerichtetem Graphen als auch bei gerichteten Graphen mindestens eine Eingangskante besitzen muss.

 Ecken und Kanten eines zusammenhängenden Graphens

Da jeder Kante zwei Knoten/Ecken benötigt, darf die Anzahl der Kanten (E) maximal um den Betrag von 1 |1| geringer sein als die Anzahl Ecken (V). Diese Eigenschaft lässt sich anhand eines Graphens mit 2 Knoten verdeutlichen. 2 Knoten können maximal eine Kante bilden. Somit hat jeder Knoten maximal eine Eingangskante. Wäre die Mindest-Anzahl der Kanten nicht kleiner als die Anzahl der Knoten, würde sich bei unserem Graphen mit 2 Knoten und einer Kante bei gleicher Anzahl von Knoten und Kanten jeweils einen Widerspruch ergeben.

• Zwei (ungerichtete) Kanten können nicht von zwei Ecken gebildet werden.
• 1 Knoten kann keine Kante erzeugen (Schleifen ausgenommen)

Arithmetische Eckeneigenschaften eines Graphens

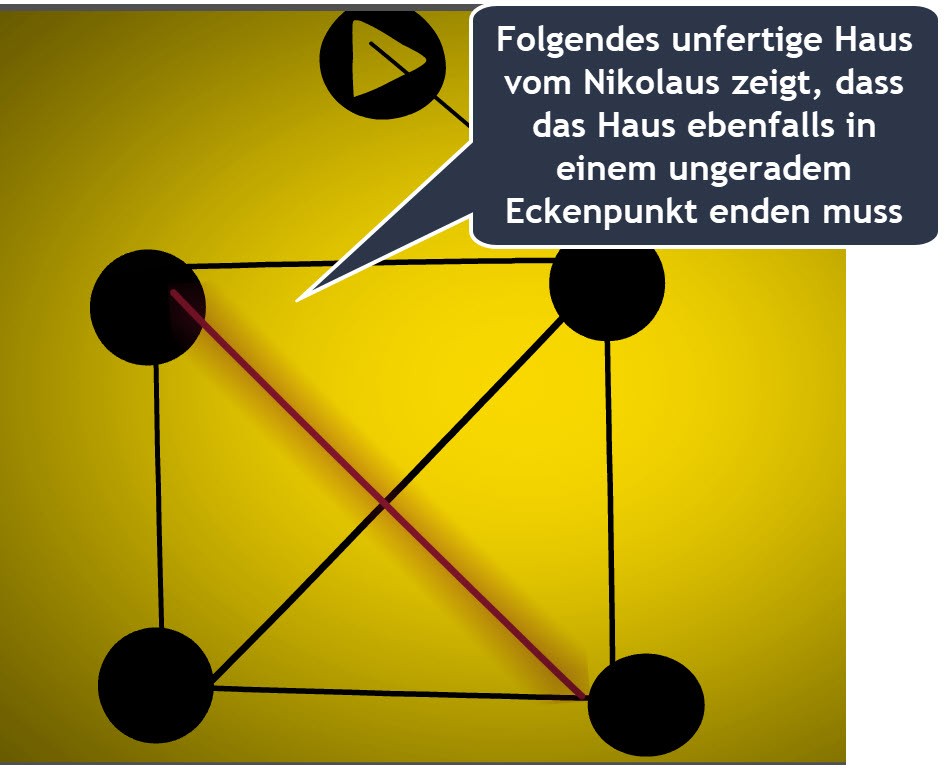
Hast du dich schon einmal gefragt, warum du beim Zeichnen des Hauses vom Nikolaus immer entweder unten links oder unten rechts anfangen musst?

Nach diesem Artikel kennst du die Antwort, also bleib dran und abonniere unseren Youtube Kanal wenn du wissenswerte Videos zum Themen Wirtschaft, Finanzen und Informatik nicht verpassen willst.

Um sich den arithmetischen Eckeneigenschaften eines Graphens bewusst zu werden, eignet sich wie bereits erläutert das typische Beispiel vom Haus des Nikolaus.

Falls du die Regeln beim Zeichnen des Hauses vom Nikolauses nicht kennst, bist du absolut lost.

Nichtsdestotrotz nocheinmal die Regeln:

Wenn du das Haus vom Nikolaus zeichnest, gilt die Regel, dass du nicht absetzen darfst und keine Kante doppelt zeichnen darfst.

Weg-Ziel-Äquivalenz ungerichtete Graphen

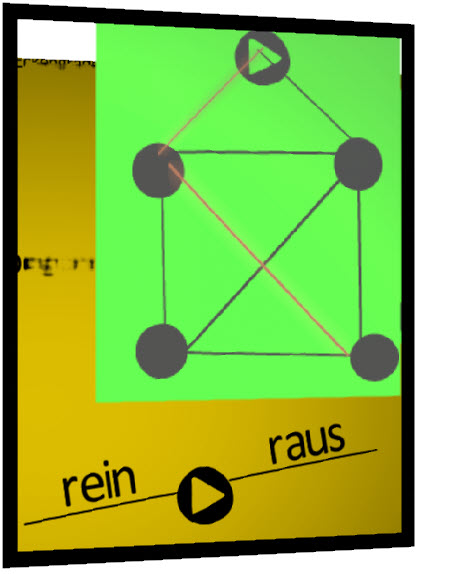
Bei einem ungerichteten Graphen startest du die Zeichnung im mit dem Playbutton gekennzeichneten Knoten und mündest bei Vollendung des Hauses des Nikolauses unten links.

Da der Graph ungerichtet ist, könnten wir den Weg auch einfach rückwärtslaufen, dann wäre die untere linke Ecke vom Haus der Startpunkt und die rechte untere Ecke der Endpunkt.

Untersuchungsaspekt Eckengrade 

Anzahl ungerader Eckengerade

Wenn wir die Eckengrade der Knoten vom Haus des Nikolaus bestimmen, d.h. wir zählen die Anzahl der Kanten die mit einem Knoten verbunden sind, stellt sich heraus, dass bis auf Endpunkt und Startpunkt des Zeichenpfades vom Haus des Nikolaus alle Knoten einen graden Eckengrad aufweisen.

Eckengerade von Start & Ziel ungerade – Warum?

Doch warum genau haben ausschließlich Start- und Endpunkt einen ungeraden Eckengrad?

Und warum haben alle anderen Knoten einen geraden Eckengrad?

Diese Fragen lassen sich beantworten, wenn man die arithmetischen Eigenschaften eines Graphens untersucht.

Minimalgrad und Maximalgrad

Um diese bestimmen zu können, bestimmen wir zunächst den Minimalgrad und Maximalgrad des Hauses vom Nikolaus, d.h. wir bestimmen den Knoten mit der geringsten und höchsten Anzahl an aneckenden Kanten im wortwörtlichen Sinn und zählen eben jene Kantenanbindung.

Anschließend bestimmen wir die Anzahl der geraden und ungeraden Eckengrade der Knoten.

Der Minimalgrad beträgt 2 und ist gerade.

Der Maximalgrad ist 4 und ist ebenfalls gerade und darüber hinaus doppelt so hoch wie der Minimalgrad.

  Anzahl der Eckengrade untersuchen

Anzahl gerader und ungerader Eckengerade

Anzahl der Ecken mit geradem Grad beträgt:  3

Implikation:

Die Anzahl von Ecken mit geradem Grad darf ungerade sein.

Anzahl der Ecken mit ungeradem Grad beträgt: 2

Implikation:

Die Anzahl von Ecken mit ungeradem Grad darf gerade sein.

Hypothese 1

Die Anzahl von Ecken mit ungeradem Grad MUSS gerade sein.

Anhand der Feststellung, dass die Anzahl der Ecken mit ungeradem Eckengrad den Wert 2 beträgt und somit gerade ist, lässt sich mit der Hypothese verknüpfen, dass zur Verhinderung einer redundanten Kanten-Zeichnung das Haus vom Nikolaus mit einer Ecke mit einem ungeradem Eckengrad beginnen muss.

Hypothese 2

Das Haus vom Nikolaus muss mit einer Ecke mit einem ungeradem Eckengrad beginnen

Ebenso lässt sich bei der Zeichnung des Hauses vom Nikolaus erkennen, dass der Endpunkt keinen geraden Eckengrad besitzen kann.

Selbiges lässt sich auch ohne Probezeichnungen beweisen, da der Endpunkt bei einem ungerichteten Graphen äquivalent ist zum Startpunkt, da die Kanten keine Richtung haben und der Weg vom ursprünglichen Startpunkt zum ursprünglichen Endpunkt genauso gut umgekehrt werden kann.

Hypothese 3

Das Haus vom Nikolaus muss mit einer Ecke mit einem ungeradem Eckengrad enden.

Vereinigung der Hypothesen

Die Anzahl von Ecken mit ungeradem Grad MUSS gerade sein.

Das Haus vom Nikolaus muss mit einer Ecke mit einem ungeradem Eckengrad starten und enden

Abbildung 1: Beispiel für Problematik wenn Haus in Knoten mit geradem Eckpunkt endet

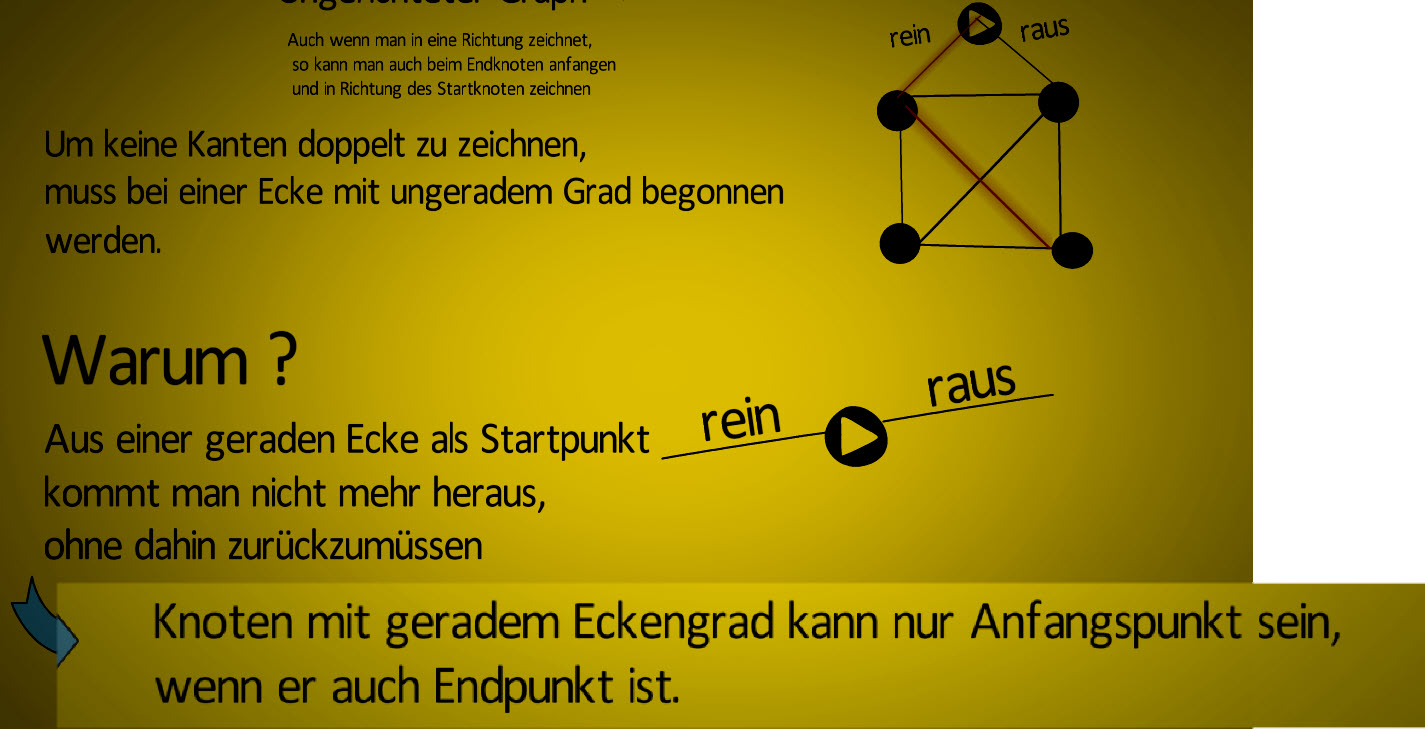
Um zu verstehen, warum das Haus von Nikolaus mit einem Knoten mit ungeradem Eckengrad beginnen und enden muss, lohnt sich der Blick auf den einzelnen Knoten.

Bei einem einzelnen Knoten mit einem geraden Eckengrad als Anfangspunkt, in diesem Fall mit dem Eckengrad 2 Beispiel, müsste der Knoten ebenfalls auch Endpunkt sein.

Dies ist damit zu begründen, dass ein ausgehender Weg bzw. eine Ausgangskante dem Knoten den Eckengrad 1 verleiht.

Um einen Eckengrad von 2 bzw einen geraden Eckengrad zu erhalten, muss also auch wieder ein Weg zum Knotenpunkt zurückführen. Da beim Haus vom Nikolaus jeder Weg bzw. jede Verbindungskante nur einmal durchlaufen werden darf, muss der Knotenpunkt also über eine Verbindungskante respektive Eingangsweg verfügen, welche in ihm mündet.

Würde die Eingangskante nicht in dem Startpunkt münden und stattdessen durch einen weiteren Ausgangsweg aus dem Startknoten heraus den Startpunkt jedeglich als Durchlaufpunkt nutzen, wäre zwar gewährleistet, dass der Knoten ein Startpunkt und nicht gleichzeitig Endpunkt ist, dafür hätte er jedoch drei Eckpunkte und wäre ungerade.

Somit lässt sich festhalten:

Knoten mit geradem Eckengrad sind im Kontext von Wegen innerhalb von ungerichteten Graphen immer entweder Zwischenknoten oder aber Start- und Endpunkt zugleich.

Diese Aussage impliziert, dass Knoten mit ungeradem Eckengrad immer Anfangs- oder Endknoten sein müssen wenn Eingangs- und Ausgangsknoten nicht der gleiche Knoten sind, wie z.B im Falle des Hauses vom Nikolaus.

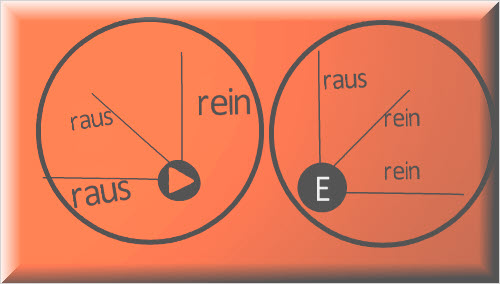
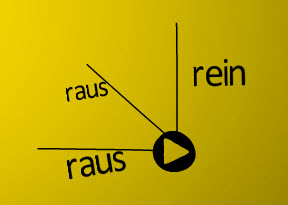
Bei einem Eckengrad von 3 gilt

raus, rein, raus

oder rein, raus, rein (Endpunkt)

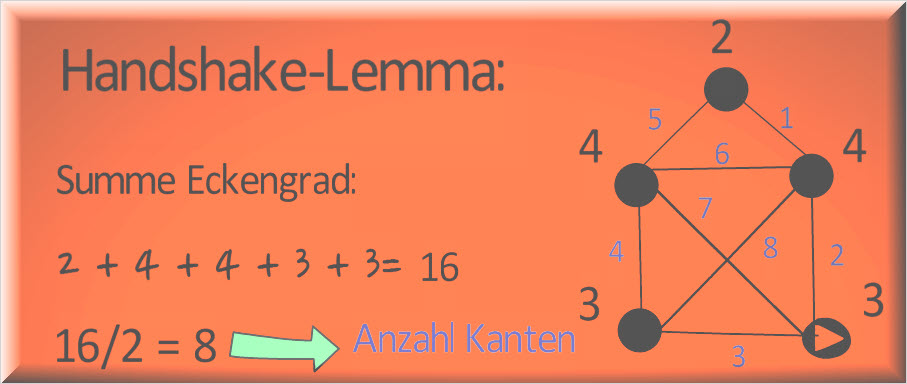
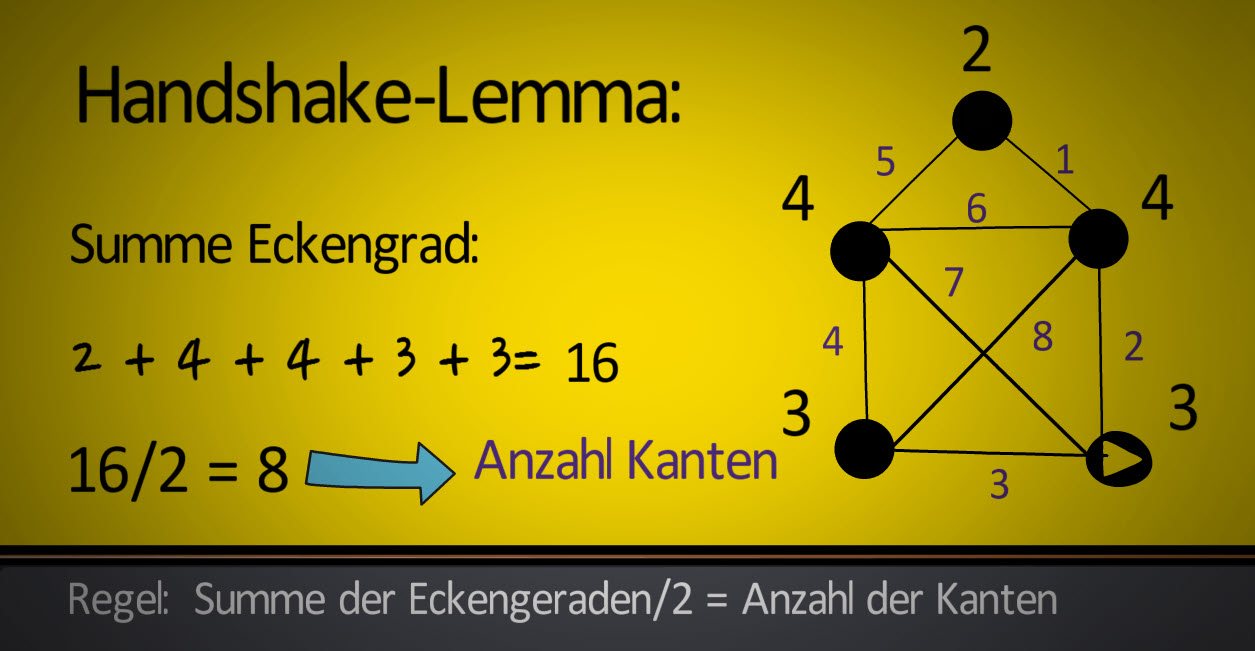
Der Zusammenhang zwischen Kantenanzahl und Eckengrad wird auch als Handshake-Lemma bezeichnet.

Handshake Lemma

Genauso wie bei einem Handschlag zwei Hände notwendig sind, sind bei einem Graphen immer zwei Knoten notwendig um eine Verbindungskante zu bilden.

Dies gilt unabhängig davon, ob die Kante gerichtet oder ungerichtet ist, sofern die Eckengrade beim gerichteten Graphen wie folgt berechnet werden:

|eingangskante d(x) + + ausgangskante d(x) - |für ungerichtete Graphen

Das Handshake Lemma besagt, dass bei zusammenhängenden Graphen die Summe aller Eckengrade dividiert durch 2 die Anzahl der Kanten ergibt.

Zusammenhängende Graphen sind Graphen, bei denen jeder Knoten von jedem anderen Knoten direkt oder indirekt erreicht werden kann.

Warum die Summe der Eckengrade gerade ist

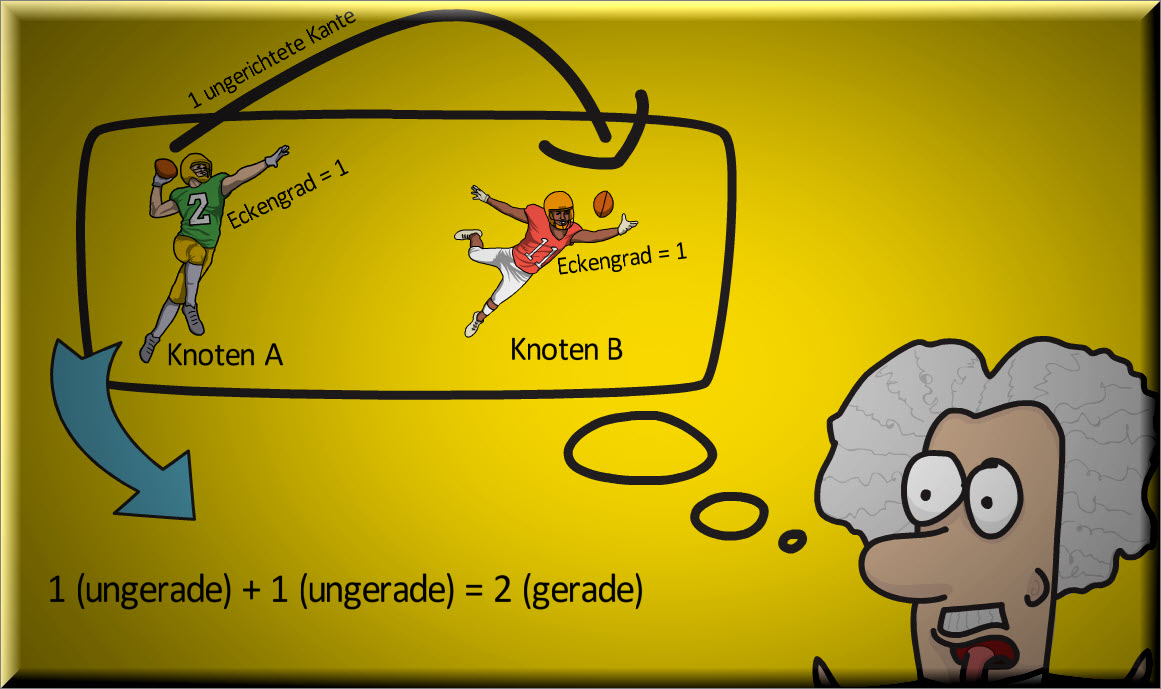
Abgeleitet aus dem Handshake Lemma lässt sich nachweisen, dass die Summe der Eckengrade eines ungerichteten Graphens stets eine gerade Zahl sein muss

Damit eines Knoten einen Eckengrad von 1 besitzt, muss dieser eine Verbindungskante zu einem anderen Knoten aufweisen.

Dies lässt sich sehr schön anhand eines Passes aufzeigen. Ein Pass kann nur dann vollendet werden, wenn Spieler A den Ball zu Spieler B wirft und dieser den Ball fängt.

Ein pass bedingt also immer zwei Akteure, genauso wie eine Kante immer zwei Knoten benötigt.

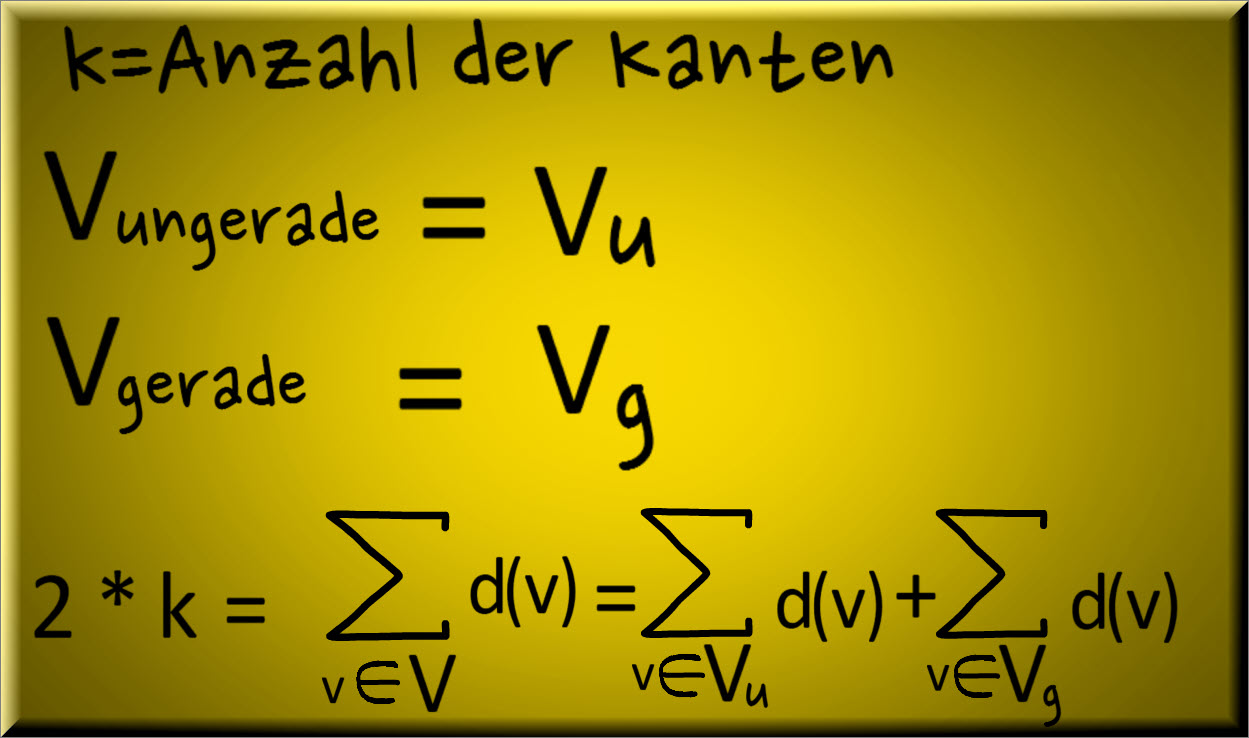
Formaler Schreibweise

Der Eckengrad bei einem ungerichteten Graphen wird mit d(v) beschrieben.

Beim formalen Beweis differenzieren wir zwischen den Knoten mit ungeradem Eckengrad (Vu) und Knoten mit geradem Eckengrad (Vg).

k bezeichnet die Anzahl der Kanten in einem Graphen.

Die obige Formel bedeutet gesprochen:

Die Anzahl der Kanten multipliziert mit Faktor 2 ergibt die Summe aller Eckengrade der Knotenmenge V.

Die Summe aller Eckengrade der Knotenmenge V setzt sich zusammen aus der Summe der ungeraden Eckengrade und der geraden Eckengrade.

Nachweis am Beispiel vom Haus vom Nikolaus

Der obig formal definierte Zusammenhang zwischen Knoten, Kanten und Eckengraden lässt sich hervorragend am Haus vom Nikolaus veranschaulichen, da dieses als ein ungerichteter zusammenhängender Graph modelliert werden kann.

Die Anzahl der Kanten beträgt 8. Verdoppelt man diesen Betrag gelangt man zur Summe aller Eckengerade, welche sich in zwei Teilmengen aufteilen lässt.

Die erste Teilmenge wird gebildet aus der Summe aller ungeraden Eckengeraden – in diesem Fall die Eckengeraden des Start- und Endknotens vom Haus des Nikolaus mit einem Eckengrad von jeweils 3.

Die zweite Teilmenge entspricht der Summe aller geraden Eckengrade und enthält somit die Eckengerade aller „Durchlaufknoten“.

Warum die Summe ungerader Eckengerade gerade sein muss

Die Tatsache, dass die Anzahl der Eckengerade in einem (ungerichtetem zusammenhängendem) Graphen gerade ist, impliziert, dass die Anzahl der Knoten mit ungeradem Eckengrad ebenfalls gerade sein muss.

Dies ist insofern logisch, als dass eine ungerade Anzahl an Knoten mit ungeradem Eckengrad eine ungerade Summe an Eckengeraden ergibt.

Addiert man diese ungerade Summe mit der geraden Summe aller geraden Eckengerade erhält man wiederum eine ungerade Summe.

Da die Gesamtsumme aller Eckengerade jedoch gemäß Pumping Lemma gerade sein muss, ergibt sich ein Widerspruch mit der Implikation, dass die Anzahl von Knoten mit ungeradem Eckengrad selbst gerade sein muss.

Dies ist beim Haus vom Nikolaus auch der Fall.

Multipliziert man eine ungerade Zahl mit einer ungeraden Zahl, ergibt dies stets eine ungerade zahl.

Multipliert man eine ungerade Zahl mit einer graden Zahl, ergibt dies immer eine grade Zahl.

Eine Zahl kann nur ohne Rest durch eine grade Zahl (z.B 2) geteilt werden (Quotientenwert ist eine gerade Zahl), wenn die Zahl selbst grade ist.

Folglich muss ein Knoten mit ungerader Valenz (Knotengrad) immer eine gerade Anzahl haben.

Vollständigkeit von Graphen

Ein Graph ist dann vollständig, wenn jedes Paar aus der Menge der Knoten V miteinander verbunden ist.

Bei einem Graphen mit 2 Knoten existiert bei einem ungerichteten Graphen eine Kantenanzahl von 1.

Bei einem Graphen mit 3 Knoten existiert bei einem ungerichteten Graphen eine Kantenanzahl von 2

Wir erstellen gerade Inhalte für diese Seite. Um unseren eigenen hohen Qualitätsansprüchen gerecht zu werden benötigen wir hierfür noch etwas Zeit.

Bitte besuchen Sie diese Seite bald wieder. Vielen Dank für ihr Interesse!